Objetivos da atividade
O objetivo desta atividade é realizar uma análise de frequência de cheias a nível local. Isso significa que iremos relacionar a magnitude das vazões máximas anuais com a probabilidade da mesma ser excedida. A análise a nível local siginifca que utilizaremos apenas as informações de vazão observadas na estação fluviométrica de interesse, sem fazer uso de informações sobre as vazões máximas anuais que teham acontecido em outras estações fluviométricas localizadas na região.
Além de construirmos a relação entre a magnitude das vazões máximas anuais e a respectiva probabilidade de excedência, é importante saber estimar também o grau de incerteza nessas estimativas. Essas incertezas são usualmente representadas por intervalos de confiança, como veremos mais adianate.
Além de calcular essas quantidades, a curva de frequência, e suas respectivas incertezas, são representadas graficamente, como na figura abaixo, que mostra os resultados para um estudo de cheias numa seção do Rio Salado, localizada na província de Santa Fé, na Argentina, onde em 2003 ocorreu o rompimento de um dique que resultou em perde de vidas humanas e elevados prejuízos. Nesse caso, utilizou-se a distribuição Generalizada de Valores Extremos (GEV), mas aqui no curso faremos uso de uma distribuição mais simples de se trabalhar, a lognormal. O objetivo aqui é ter uma motivação hidrológica para apreder a usar a linguagem R.
Contruiremos aqui no curso uma figura semelhante a esta, onde no eixo-x temos o tempo de recorrência e no eixo-y a magnitude das vazões máximas anuais. O tempo de recorrência apresentado no eixo-x é uma maneira de representar a probabilidade de excedência. A linha cheia em vermelho representa o valor esperado dos valores da vazão máxima anual em função do tempo de recorrência, enquanto as linhas tracejadas representam os intervalos de confiança de 95%, ilustrando as incertezas envolvidas nessas estimativas. Os círculos azuis escuros representam as vazões máximas anuais registradas no passado, enquanto o círculo azul claro mostra a cheia destruidora de 2003.
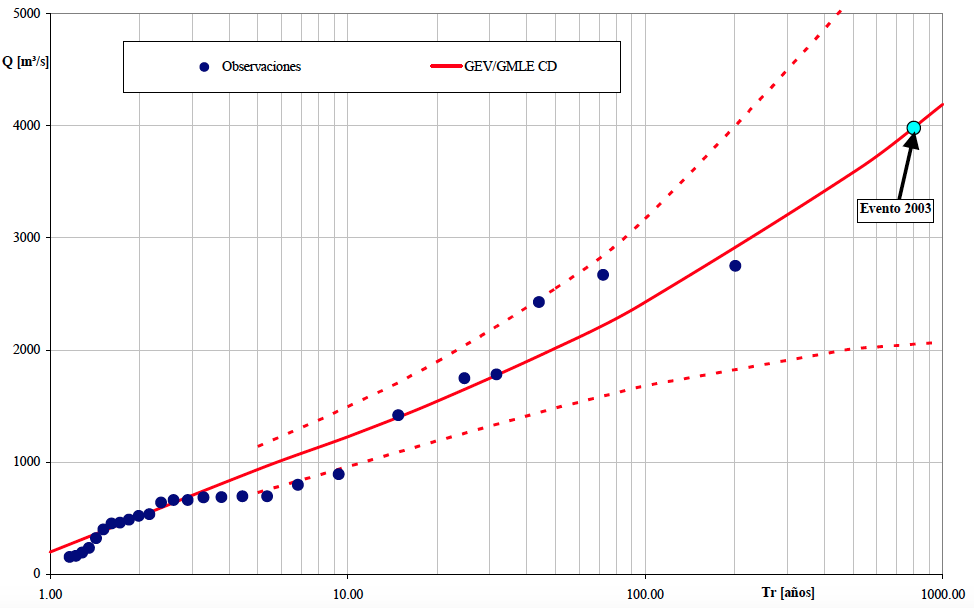
(#fig:curva_freq)Curva de frequência do cheias do Rio Salado, na Argentina.
Seleção das vazões máximas anuais
O primeiro passo de nossa atividade consiste em obter a série de máximos anuais que desejamos analisar. A obtenção da série de máximos anuais será realizada em duas etapas. Primeiro vamos obter a séries de vazões diárias, e para isso utilizaremos a mesma função de obtenção de séries diárias de vazão que aprendemos na segunda aula deste curso. Com a série de vazões diárias em mãos, passaremos para a segunda etapa, que é a de extrair a vazão máxima de cada ano hidrológico.
Obtenção da série de vazões diárias
A função abaixo permite obter a série de vazões diárias de uma estação fluviométrica. O único argumento desta função é o código da estação. Quando chamamos esta função, ela retorna um dataframe com 3 colunas: o código da estação, a data, e o valor da vazão diária.
Como já estudamos esta função anteriormente, a uitlizaremos aqui sem entrar em qualqer detalhes sobre seu funcionamento.
# Função para obter série histórica de vazão de uma determinada estação ####
dados_serie_ANA <- function(cod_estacao = NA,
data_inicio = "01/01/1800",
data_fim = Sys.Date(),
tipo_dados = 3,
nivel_consist = 1){
# Pegar dados a partir do url e transformar em um dataframe
url_base <-
paste0("http://telemetriaws1.ana.gov.br/ServiceANA.asmx/",
"HidroSerieHistorica?",
"codEstacao=", cod_estacao,
"&dataInicio=", data_inicio,
"&dataFim=", data_fim,
"&tipoDados=", tipo_dados,
"&nivelConsistencia=", nivel_consist)
url_parse <- XML::xmlParse(url_base, encoding = "UTF-8")
node_doc <- XML::getNodeSet(url_parse, "//SerieHistorica")
dados_estacao <- XML::xmlToDataFrame(nodes = node_doc)
# Por algum motivo o hidroweb não está filtrando os dados pela consistencia
dados_estacao <- filter(dados_estacao, NivelConsistencia == nivel_consist)
# Separar data e hora
dados_estacao$Data <- as.Date(substr(dados_estacao$DataHora, 1, 10))
dados_estacao$Hora <- substr(dados_estacao$DataHora, 12, 19)
# Fazer um dataframe só com datas e valores de vazão
datas_dia <- seq.Date(from = min(dados_estacao$Data),
to = max(dados_estacao$Data) %m+% months(1) - 1,
by = "day")
tabela_final <- data.frame(Cod_estacao = dados_estacao$EstacaoCodigo[1],
Data = as.character(datas_dia),
Vazao = as.numeric(NA))
for(i in 1:nrow(tabela_final)){
# Dia em análise
dia <- as.numeric(substr(tabela_final$Data[i], 9, 10))
# Mês e ano em análise
mes_ano <- as.Date(paste0(substr(tabela_final$Data[i], 1, 8), "01"))
# Olhar a linha do mes e ano e escolher a coluna pelo dia + 15
linha_dado <- which(dados_estacao$Data == mes_ano)
# Se não tiver o mês nos dados da estação, colocar valor NA
ifelse(length(linha_dado) == 0,
tabela_final$Vazao[i] <- NA,
tabela_final$Vazao[i] <-
as.numeric(dados_estacao[linha_dado, (dia + 15)]))
}
return(tabela_final)
}Precisamos escolher uma estação fluviométrica para realizar nossa análise. Sugiro utilizar a estação 60435000, localizada na bacia do Rio Descoberto, que drena uma área de 113.2 km\(^2\), mas vocês têm a indepedência de escolhar qualquer outras estação que esteja no banco de dados da Agência Nacional de Águas.
Para obter a série diária da estação escolhida, basta chamar a função acima passando o argumento necessário, que é simplesmente o código da estação desejada. A função devolve um dataframe com a série de vazões médias diárias.
Para fins de visualização, utilizamos a função head(nome_do_dataframe) do R, como mostrado abaixo, que nos mostra as primeiras 6 linhas do dataframe.
dados_60435000 <- dados_serie_ANA(cod_estacao = 60435000)
index_falha_diario <- which(is.na(dados_60435000[,3]==TRUE))
dias_falha <- dados_60435000[index_falha_diario,2:3]
head(dados_60435000) Cod_estacao Data Vazao
1 60435000 1978-05-01 NA
2 60435000 1978-05-02 NA
3 60435000 1978-05-03 NA
4 60435000 1978-05-04 NA
5 60435000 1978-05-05 NA
6 60435000 1978-05-06 NAAlém disso, é sempre importante visualizar os dados para que se teha uma ideia geral da faixa de variação das vazões, sazonalidade e outras padrões que possa ser percebidos num gráfico.
Aqui, nós plotaremos a série completa das vazões diárias da estação 60435000 utilizando o código abaixo, que emprega o chamado R-base, ao invés de pacote ggplot2, visto na aula anterior. Mas se preferir utilizar o ggplot2 para realizar esta plotagem, fique à vontade.
time <- as.Date(dados_60435000$Data)
plot(time,dados_60435000$Vazao,type="l",
main = "Vazões diárias - estação 60435000",
xlab = "Anos",ylab = "Q (m3/s)")
# Adiciona grid horizontal apenas
grid(nx = NA, ny = NULL,
lty = 2, # Grid line type
col = "gray", # Grid line color
lwd = 2) # Grid line width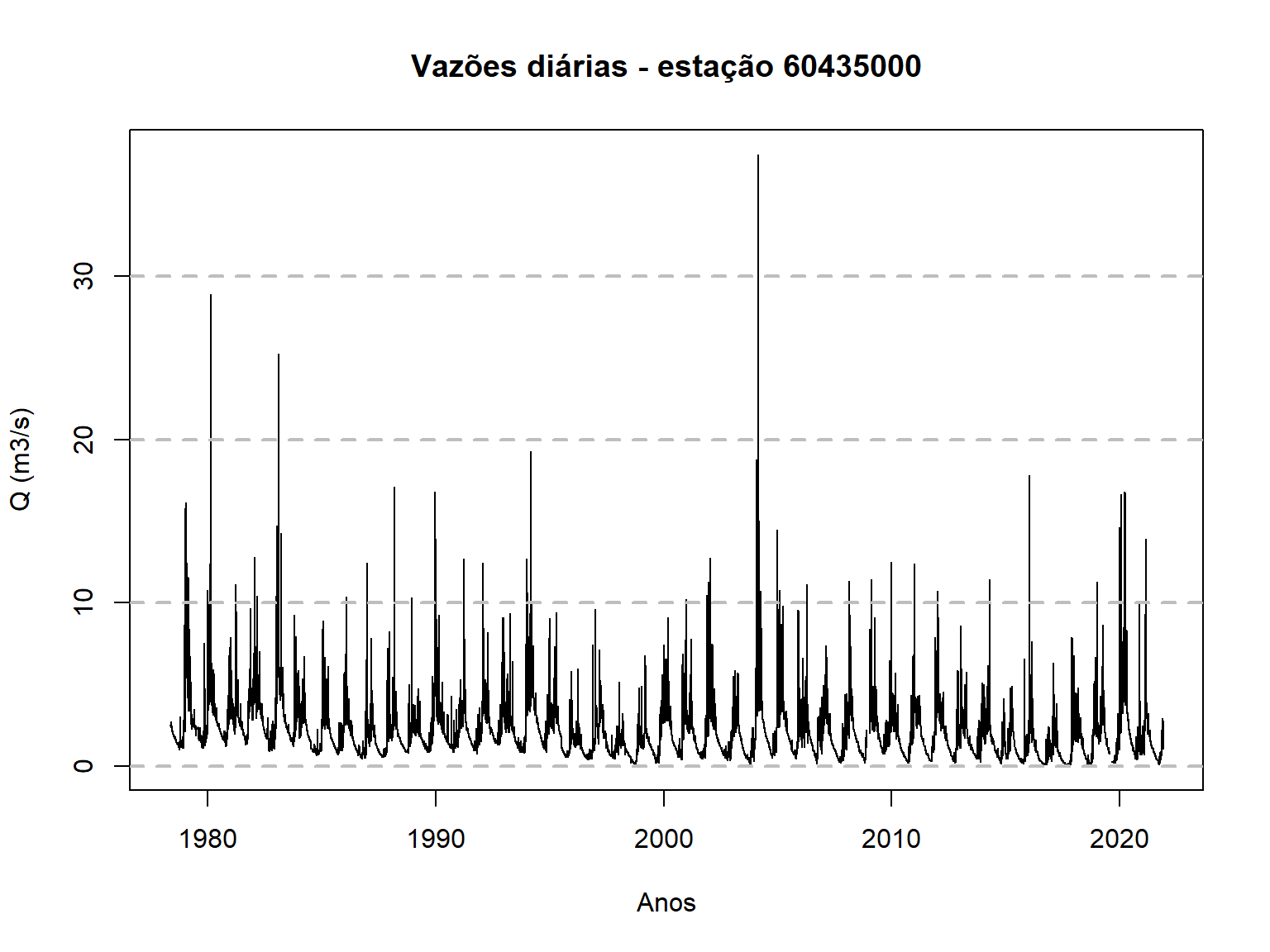
Extração da série de vazões máximas anuais
Com a série de vazões diárias, passamos ao segundo passo que é o de construir a série de máximos anuais com base no ano hidrológico. Para isso, utilizaremos uma outra função, que é apresentada abaixo. Veja que a função tem como default o ano hidrológico com início no mês de agosto. Mas o mês de início do ano hidrológico pode ser facilmente alterado, bastando aicionar esse argumento quando chamar a função.
# Contrução da série de máximos anuais a partir de um ano hidrológico ####
fun_max_ano <- function(tabela = NA,
comeco_ano_hidro = 8){
# Transformar a coluna Data em "Dates" (caso esteja em character)
tabela$Data <- as.Date(tabela$Data)
# Definir se o mês em questão entra no ano atual ou no próximo ano
desloc_ano <- ifelse(month(tabela$Data) < comeco_ano_hidro, 0, 1)
# Ano Hidro
tabela$ano_hidro <- year(tabela$Data) + desloc_ano
# Fazer uma tabela final apenas com os máximos anuais
max_anuais <-
tabela %>%
group_by(Cod_estacao, ano_hidro) %>%
summarise(maxima = max(Vazao))
}Para finalmente obtermos a série de máximos anuais, basta chamar a função fornecendo o arquivo que contém as séries diárias de vazão, que no nosso caso é o dados_60435000. Mais uma vez, podemos utilizar a função head para dar uma leve espiada nas informoações contidas no dataframe.
Q_max <- fun_max_ano(dados_60435000)
head(Q_max)# A tibble: 6 × 3
# Groups: Cod_estacao [1]
Cod_estacao ano_hidro maxima
<chr> <dbl> <dbl>
1 60435000 1978 NA
2 60435000 1979 16.1
3 60435000 1980 28.9
4 60435000 1981 11.1
5 60435000 1982 12.8
6 60435000 1983 25.3A função fun_max_ano foi escrita de forma que qualquer falha na série de vazões diárias num dado ano hidrológico resulta numa falha na série de máximos anuais. Isso nem semrpe é necessário, já que falhas no período de estiagem não indicam falhas nas séries de máximos, mas creio que a função nos serve bem para este curso.
Podemos notar a presença de um NA na nossa plotagem acima. É interessante verificar o número total de anos disponíveis com dados diários de vazão, bem como o número de anos com falha na série de máximos anuais.
O número de anos com dados de vazões diárias pode ser obtidos simplemente identificando o número de linhas no dataframe Q_max, e para isso utilizamos o código abaixo,
n_anos <- nrow(Q_max)
n_anos[1] 48Mas já sabemos que o ano de 1978 não contém o valor de vazão máxima porque a série de vazões diárias não estava completa. Será que há outros anos no histórico com esse problema? Para identificar se há falha em outros anos, utilizaremos duas funções do R de forma conjunta, is.na e which. A função is.na identifica se o elemento é um NA ou não, retornando um valor lógico, TRUE ou FALSE, enquanto a função which permite identificar a posição de uma dada condição. O código abaixo permite identificar em quais anos ocorrem falhas na série de máximos anuais,
# A tibble: 6 × 2
ano_hidro maxima
<dbl> <dbl>
1 1978 NA
2 2009 NA
3 2020 NA
4 2022 NA
5 2023 NA
6 2024 NAA primeira linha de código identifica as posições em que há a presença de NA na terceira coluna do dataframe, que é a coluna com as informações sobre as vazões máximas de cada ano hidrológico, e associa à variável index. Na linha seguinte, criamos um novo dataframe com a informação dos anos em que temos falhas nos dados.
É verdade que poderíamos ter escrito o código acima de uma forma mais compacta, porém ficaria mais difícil de entender. Veja o que você acha.
# A tibble: 6 × 2
ano_hidro maxima
<dbl> <dbl>
1 1978 NA
2 2009 NA
3 2020 NA
4 2022 NA
5 2023 NA
6 2024 NAMais à frente, quando tivermos que fazer os cálculos necessários para realizar a análise de frequência, teremos que nos livrar desses anos com falhas. Mas por enquanto, vamos deixá-los como estão, e passemos `a etapa seguinte que é a de visualizar a série de máximos anuais.
Visualização da série de máximos anuais
Agora já podemos visualizar a série de máximos anuais que serivirão de base para a nossa análise de frequência. Essa visualização pode ser feita com o código abaixo, que utiliza apenas o R-base. Mais uma vex, se desejar utilizar o ggplot2 para essa plotagem, fique à vontade.
plot(Q_max$ano_hidro,Q_max$maxima,type = "o",
main = "Máximos anuais - 60435000",
xlab = "Anos",ylab = "Q_max (m3/s)",lwd = 2)
# Adiciona grid
grid(nx = NULL, ny = NULL,
lty = 2, # Grid line type
col = "gray", # Grid line color
lwd = 1) # Grid line width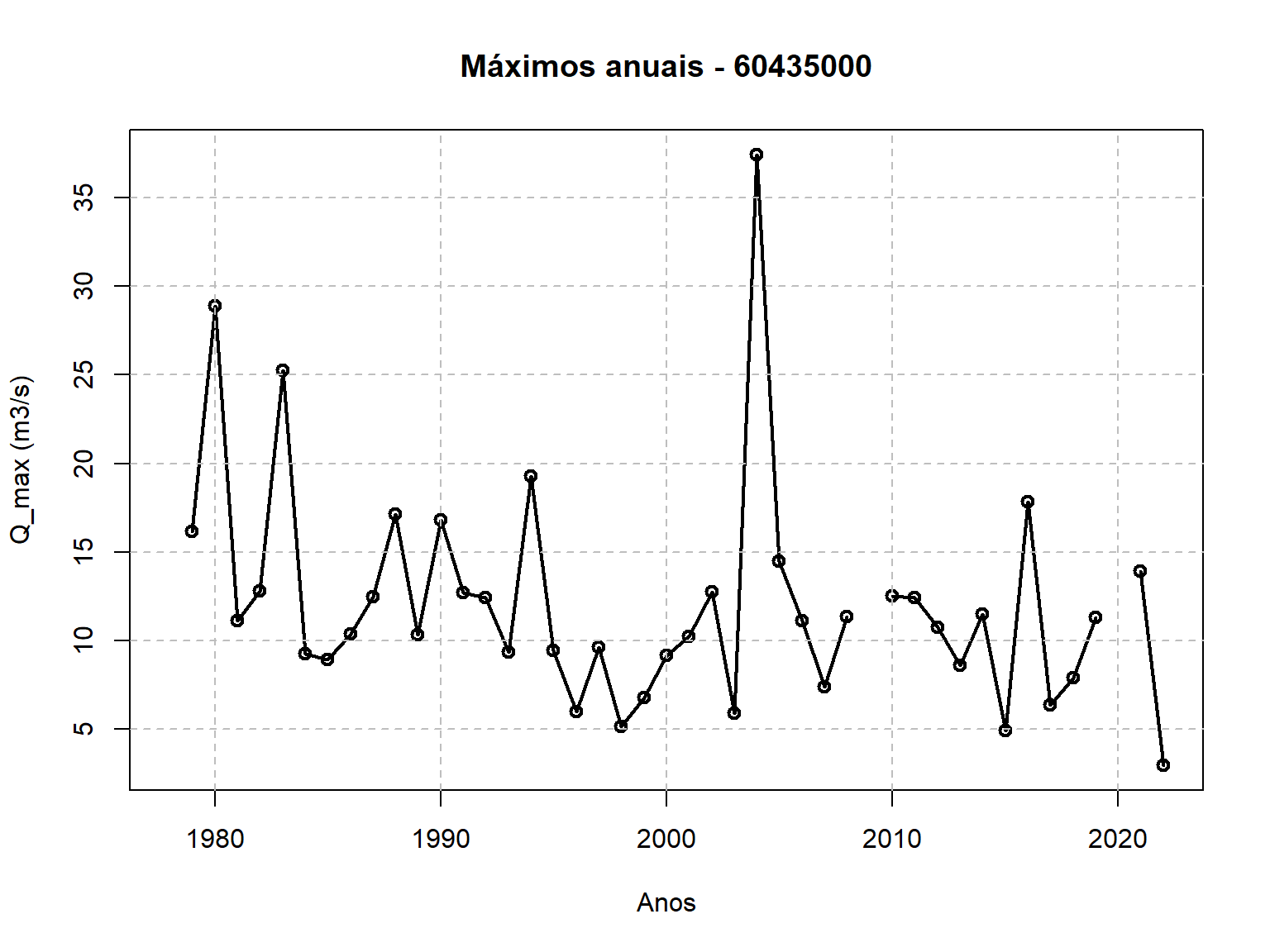
Construção da curva de frequência amostral
Posição de plotagem
Para que possamos plotar os círculos azuis escuros da Figura apresentada anteriormente, para o caso do Rio Salado, que representam as vazões máximas anuais observadas na série histórica, precisamos determinar as chamadas posição de plotagem, que servirão de base para o cálculo do tempo de recorrência empírico para cada valor de vazão da amostra.
Para que seja possível entender esta etapa, vale a pena investir um certo tempo do curso em alguns conceitos básicos.
O tempo de recorrência associado a uma determinada magnitude de vazão, \(T_r(q)\), é um conceito hidrológico bastante conhecido, de forma que não dedicaremos muito tempo para discutí-lo aqui. Por definição, o tempo de recorrência de um evento, cuja magnitude vale \(q\), é igual ao inverso da probabilidade da vazão máxima anual exceder esse valor,
\[T_r(q) = \frac{1}{P(Q>q)}\]
Por exemplo, se a probabilidade da vazão máxima anual ultrapassar um dado valor \(q\) for igual a 0.10, dizemos que o tempo de recorrência dessa vazão \(q\) é de 10 anos. Da mesma forma, se \(P(Q>q)=0.01\), dizemos que o tempo de recorrência de \(q\) vale 100 anos.
Portanto, para que possamos incluir as vazões observadas na nossa curva de frequência, será preciso determinar a probabilidade de excedência de cada uma das observações contidas na série de vazões máximas anuais da localidade de interesse. Como o intuito neste primeiro momento é plotar as vazões observadas na curva de frequência, nos basearemos na chamada distribuição empírica de frequência.
A distribuição empírica de frequência relaciona cada valor de vazão máxima observada na série histórica, denominada aqui de \(q_i\), com sua frequência relativa acumulada, \(\hat{F}_Q(q_i)\). A quantidade \(\hat{F}_Q(q_i)\) representa a nossa estimativa para a probabilidade da variável de interesse, \(Q\), ser menor ou igual ao valor amostral, \(q_i\),
\[\hat{F}_Q(q_i) = \hat{P}(Q \le q_i)\]
em que \(\hat{F}_Q\) é a estimativa da frequência relativa acumulada da variável aleatória \(Q\) baseada na amostra, enquanto \(q_i\) representa o valor de uma dada observação \(i\). O uso do acento circunflexo na equação acima é uma convenção utilizada em estatística para mostrar que estamos nos referindo a uma estimativa da grandeza em questão baseada na amostra que se tem em mãos.
Já dissemos acima que o tempo de recorrência \(T_r(q)\) é função da probabilidade de excedência, que por sua vez pode ser interpretada como o complemento de \(F_Q(q_i)\). Dessa forma, podemos dizer que
\[\hat{P}(Q \gt q_i) = 1 - \hat{P}(Q \le q_i)\] de forma que
\[\hat{T}_r(q_i) = \frac{1}{1-\hat{P}(Q \le q_i)}\]
Pode parecer estranho se você estiver vendo isso pela primeira vez, mas a verdade é que há diferentes maneiras de se estimar a distribuição empírica de frequência das observações de uma amostra, \(\hat{P}(Q\le q_i)\), ou seu complemento, \(\hat{P}(Q\gt q_i)\).
Uma maneira bem comum de estimar tais probabilidades, quando se tem uma amostra de tamanho \(n\), consiste em ordenar a série em ordem decrescente e determinar a probabilidade de excedência utilizando a seguinte fórmula,
\[\hat{P}(Q > q_{(i)}) = 1 - \hat{F}_Q(q_{(i)}) = \frac{i}{n+1}\]
em que \(q_{(i)}\) representa a chamada estatística de ordem \(i\), em que \(q_{(1)}\gt q_{(2)}\gt \ldots \gt q_{(n)}\) representa a série ordenada das vazões máximas anuais, de forma que \(q_{(1)}\) e \(q_{(n)}\) são, respectivamente, a maior e a menor observações da amostra. De acordo com essa expressão, por exemplo, numa amostra de tamanho 49, a probabilidade da vazão máxima anual ser maior do que a maior observação da amostra vale \(P(Q>q_{(1)})=0.02\)), o que resulta num tempo de recorrência de \(T_r(q_{(1)})=50\) anos.
Não se preocupe tanto se esse conceito de posição de plotagem não ficou totalmente claro. Basta saber que plotaremos os valores de máximos anuais da amostra na curva de frequência utilizando a posição de plotagem de Weibull, que é o nome que se dá à posição de plotagem \(i/(n+1)\).
Plotagem da amostra na Figura
Na verdade, utilizaremos o tempo de recorrência, \(T_r\), para plotagem, lembrando que o \(T_r\) é simplemenste o inverso da probabilidade de excedência, representada pela posição de plotagem de Weibull.
O código para o cálculo do \(Tr\) é apresentado abaixo. Para facilitar a compreenção de como o cálculo é feito, criaram-se três novas colunas ao dataframe que contém as vazões máximas anuais. Mas antes disso, efetuou-se o ordenamento das vazões máximas em ordem decrescente, ou seja, o primeiro valor de vazão da nova série ordenada é o maior da amostra.
As três novas colunas são, respectivamente, o índice das vazões, começando de 1 indo até o número total de valores, a posição de plotagem de Weilbull, que expressa a probabilidade de excedência, e por último o tempo de recorrência, \(Tr\).
# Remoção dos anos com falha
Q_max <- na.omit(Q_max)
# Ordenamento decrescente do dataframe
Q_max_ord <- Q_max[order(Q_max$maxima, decreasing = TRUE), ]
# Inclusão de Três novas colunas: index, posição de plotagem de Weibull, e Tr
Q_max_ord$index <- seq(from = 1,to = nrow(Q_max_ord))
Q_max_ord$weibull <- Q_max_ord$index/(nrow(Q_max_ord) + 1)
Q_max_ord$Tr <- 1/Q_max_ord$weibullComo já fizemos antes, podemos dar uma espiada nesse novo dataframe com as vazões máximas anuais ordenada utilizando a função head(dataframe_name),
head(Q_max_ord)# A tibble: 6 × 6
# Groups: Cod_estacao [1]
Cod_estacao ano_hidro maxima index weibull Tr
<chr> <dbl> <dbl> <int> <dbl> <dbl>
1 60435000 2004 37.5 1 0.0233 43
2 60435000 1980 28.9 2 0.0465 21.5
3 60435000 1983 25.3 3 0.0698 14.3
4 60435000 1994 19.3 4 0.0930 10.8
5 60435000 2016 17.8 5 0.116 8.6
6 60435000 1988 17.1 6 0.140 7.17A última coluna de Q_max_ord contém o valor do tempo de recorrência de cada uma das observações contidas na amostra. Vale notar que as observações em Q_max_ord estão ordenadas em ordem decrescente.
Podemos agora criar uma Figura, similar àquela apresentada para o estudo do Rio Salado. Porém, nesta etapa de nossa análise, apenas os valores amostrais das vazões máximas serão apresentados.
plot(Q_max_ord$Tr,Q_max_ord$maxima,type = "p", pch = 19,cex = 1.5,col = "blue",
log = "x",main = "Curva de frequência de cheias - 60435000",
xlab = "Tr (anos)",ylab = "Q_max (m3/s)",
xlim = c(1, 100), # X-axis limits
ylim = c(1, 50))
# Adiciona grid horizontal
axis(1, at = c(seq(1,10,by=1),seq(10,100,by=10),seq(200,1000,by=100)),
tck = 1, lty = 2, col = "gray")
# Adiciona grid vertical
axis(2, tck = 1, lty = 2, col = "gray")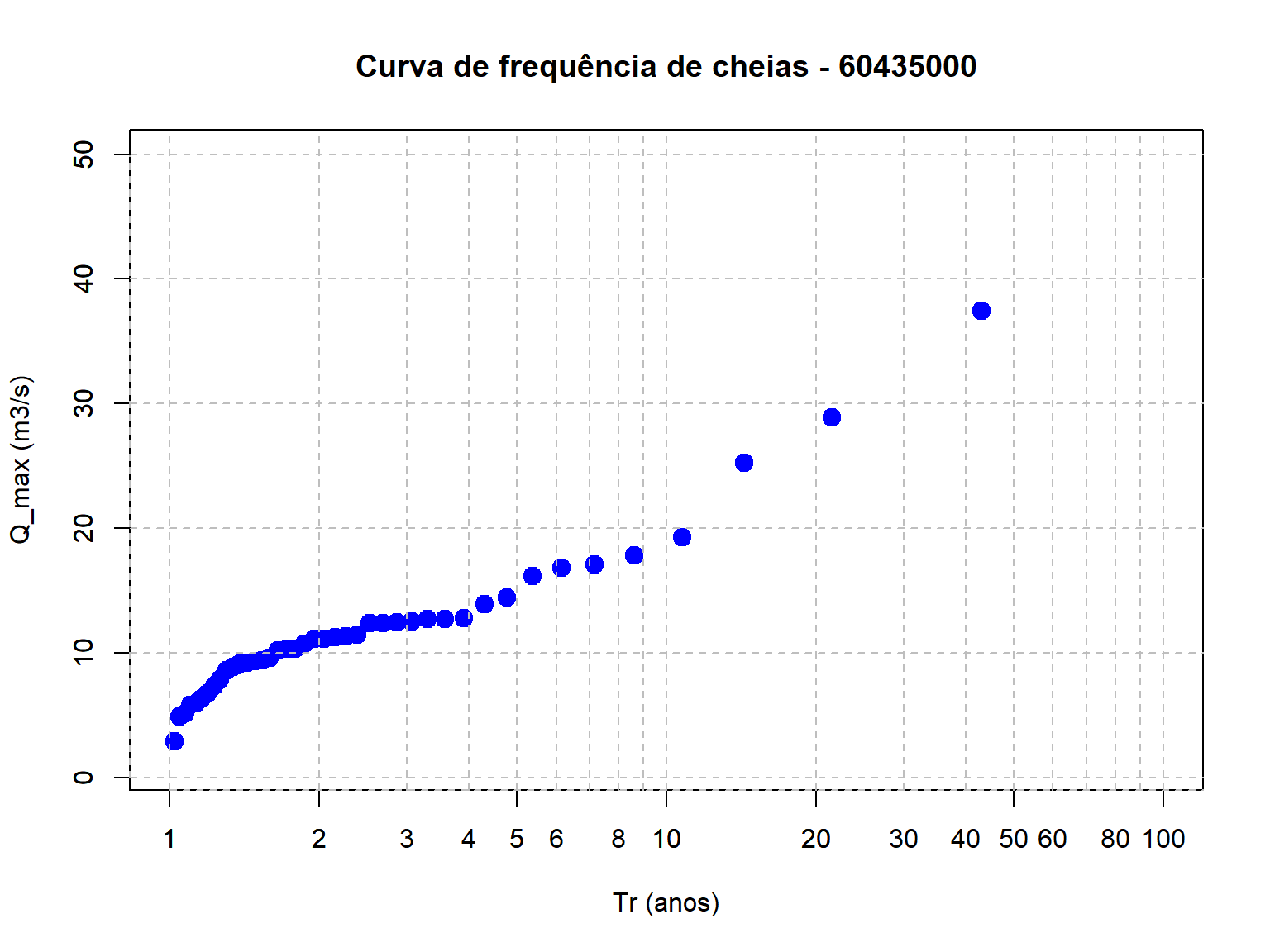
Ajuste de uma distribuição teórica de probabilidades
Estudos que realizam de análise de frequência de cheias geralmente utilizam as seguintes distribuições teóricas de probabilidade:
- Lognormal de 2 parâmetros (LN2)
- Lognormal de 3 parâmetros (LN3)
- Generalizada de Valoes Extremos (GEV)
- Log-Pearson Tipo 3 (LP3).
Como o intuito aqui não é o de se aprofundar nos detalhes técnicos de análise de frequência, o que exigiria um número muito maior de horas de aula, mas de ter uma motivação maior para aprender a linguagem R, vamos realizar nossa análise de frequência de cheias com a distribuição lognormal de 2 parâmetros, que é bastante simples de tratar.
A distribuição lognormal
Se considerarmos que as vazões máximas anuais \((Q)\) possuem uma distribuição lognormal, então os logaritmos de \(Q\), chamados aqui de \(Y = ln(Q)\), terão, por definição, uma distribuição normal,
\[ Y = ln(Q) \sim N(\mu_Y,\sigma_Y^2) \] o que significa dizer que os logarítmicos das vazões máximas anuais são bem representados por uma distribuição Normal com parâmetros \(\mu_Y\) e \(\sigma_Y^2\), que, para quem não lembra, representam a média e a variância populacionais.
O adjetivo populacional utilizado aqui é para lembrarmos que essas caracerísticas da distribuição são, na verdade, desconhecidas. A única pista que temos sobre o valor desses parâmetros está contida na amostra que temos, formada por um conjunto de vazões máximas anuais. A maneira que utilizaremos a amostra para tentar compreender essa distribuição é o assunto da seção Método de ajuste.
Quantis de cheia da lognormal
É muito provável que vocês não se recordem, mas a distribuição Normal possui uma caracterísitca bastante interessante. Se aplicarmos uma transformação linear numa variável normalmente distribuída, a nova variável continua sendo normalmente distribuída, porém com diferentes valores para os parâmetros da distribuição.
Uma transformação bastante útil é aquela em que a variável é transformada numa variável normal-padrão, usualmente representada pela letra \(Z\). A variável normal-padrão \(Z\) possui média zero e variância unitária, \(Z \sim N(0,1)\). Qualquer variável que possui distribuição Normal pode ser transformada numa variável normal-padrão, bastando subtrair sua média e dividir pelo seu desvio-padrão,
\[ Z = \frac{Y-\mu_Y}{\sigma_Y}\sim N(0,1) \]
Essa transformação é bastate útil aqui, pois utilizaremos o quantil da variável normal-padrão, \(Z_p\), para escrever o quantil de \(Y\), \(Y_p\), e também o quantil de cheia, \(Q_p\).
Quantil de uma variável aleatória, para quem não se lembra, é o valor da variável associado a uma dada probabilidade de não-excedência. Por exemplo, por definição, a probabilidade da variável aleatória \(X\) ser menor ou igual ao quantil \(x_p\) é igual a p,
\[ P(X\le x_p)=p \] Portanto, a probabilidade da variável normal-padrão, \(Z\), ser menor do que os quantis \(Z_{0.10}\), \(Z_{0.50}\) e \(Z_{0.90}\) é, respectivamente, 0.10, 0.50 e 0.90.
Como \(Z = (Y-\mu_Y)/\sigma_Y\), podemos dizer que \(Z_p = (Y_p-\mu_Y)/\sigma_Y\), de forma que
\[ Y_p = \mu_Y + Z_p\sigma_Y \] E como \(Y=ln(Q)\), podemos afirmar que
\[ Q_p = exp(\mu_Y + Z_p\sigma_Y) \] em que \(Q_p\) é o quantil populacional da variável aleatória \(Q\), que representa as vazões máximas anuais. Da mesma for que \(\mu_y\) e \(\sigma_Y\) são desconhecidos, \(Q_p\) também é. A única maneira de estimar \(Q_p\) é por meio das estimativas de \(\mu_Y\) e de \(\sigma_Y\).
Método de ajuste
Existem diversos métodos para ajustar uma distribuição teórica de probabilidades aos dados que se tem em mãos. Para o caso da distribuição lognormal com 2 parâmetros, sabe-se que uma forma eficiente de estimar os parâmetros \(\mu_Y\) e \(\sigma_Y^2\) é por meio do método dos momentos, que será explicado na sequência.
Com base numa série de vazões máximas anuais \(\{Q_1,Q_2,\ldots,Q_n\}\), determinamos uma nova série com base no logarítmos da série original, \(Y = \{Y_1,Y_2,\ldots,Y_n\}\).
Em seguida, aplicamos o métodos dos momentos para estimar \(\mu_Y,\sigma_Y^2\), o que consiste em igualar esses parâmetros aos seus valores amostrias, ou seja,
\[ \hat{\mu}_Y = \bar{Y} = \frac{\sum_1^n y_i}{n} \] e
\[ \hat{\sigma}_Y^2 = \frac{\sum_{i=1}^n (y_i - \bar{Y})^2}{n-1} \] Vale notar mais uma vez que \(\hat{\mu}_Y\) e \(\hat{\sigma}_Y^2\) possuem um acento circunflexo para indicar que eles são os estimadores amostrais dos parâmetros populacionais \(\mu_Y\) e \(\sigma_Y^2\).
Com os valores de \(\hat{\mu}_Y\) e \(\hat{\sigma}_Y^2\), podemos estimar os quantis de \(Y\) e de \(Q\),
\[ \hat{Y}_p = \hat{\mu}_Y + Z_p\hat{\sigma}_Y \] e
\[ \hat{Q}_p = exp(\hat{\mu}_Y + Z_p\hat{\sigma}_Y) \]
Ajuste da lognormal e estimativa dos quantis
Então, vamos ao que interessa. Temos basicamente que realizar três etapas para determinar os quantis de cheia com base na distribuição lognormal,
- Construir a série \(Y = ln(Q)=\{Y_1,Y_2,\ldots,Q_n\}\)
- Estimar os parâmetros \(\mu_y\) e \(\sigma_Y^2\) por meio dos estimadores \(\hat{\mu}_Y\) e \(\hat{\sigma}_Y^2\)
- Estimar os quantis de cheia, \(Q_p\), por meio do estimador \(\hat{Q}_p = exp(\hat{\mu}_Y + Z_p\hat{\sigma}_Y)\)
O código para realizar esse ajuste segue abaixo,
# Determinar a nova série Y = ln(Q)
Q_max_ord$Y <- log(Q_max_ord$maxima)
# Estimar os parâmetros da distribuição Normal, sabendo que Y ~ N(mu_y,sigma2_Y)
mu_Y_hat <- mean(Q_max_ord$Y)
sigma2_hat <- var(Q_max_ord$Y)
# Estimar os quantis de Y e de Q
p <- seq(from = 0.01,to = 0.99,by = 0.01) # define valores de p que serão empregados para os quantis
Tr <- 1/(1-p) # Calcula os tempos de recorrência para cada valro de p
z_p <- qnorm(p, 0, 1) # quantil da normal-padrão
y_p_hat <- mu_Y_hat + z_p*sqrt(sigma2_hat) # estimativa do quantil de Y
q_p_hat <- exp(y_p_hat) # estimativa do quantil de Q
# Criação de um dataframe com os quantis de cheia
Quantis_Q <- data.frame(q_p_hat,Tr)Podemos dar uma espiada no dataframe que contém os quantis de cheia utilizando a função head(dataframe.name),
head(Quantis_Q) q_p_hat Tr
1 4.095938 1.010101
2 4.605373 1.020408
3 4.960969 1.030928
4 5.246453 1.041667
5 5.490747 1.052632
6 5.707620 1.063830Podemos perceber que os seis primeiros valores dos quantis estimados não são tão interessantes, pois eles estão associados a tempos de recorrência muito baixos. Existe uma outra função no função no R que permite espiar a parte final do dataframe, ao invés da parte inicial. Essa função é chamada de tail(dataframe.name).
tail(Quantis_Q,5) q_p_hat Tr
95 22.59581 20.00000
96 23.64796 25.00000
97 25.00880 33.33333
98 26.93982 50.00000
99 30.29048 100.00000O número 5 no código acima serve para especificar quantas linhas eu estou interessado em ver.
FInalizamos esta parte da análise com a plotagem dos quantis de cheias estimados com base na distribuição lognormal,
plot(Q_max_ord$Tr,Q_max_ord$maxima,type = "p", pch = 19,cex = 1.5,col = "blue",
log = "x",main = "Curva de frequência de cheias - 60435000",
xlab = "Tr (anos)",ylab = "Q_max (m3/s)",
xlim = c(1, 100), # X-axis limits
ylim = c(1, 50))
# Adiciona a LN2
lines(Quantis_Q$Tr,Quantis_Q$q_p_hat,
col = "red",
lwd = 2)
# Adiciona grid horizontal
axis(1, at = c(seq(1,10,by=1),seq(10,100,by=10),seq(200,1000,by=100)),
tck = 1, lty = 2, col = "gray")
# Adiciona grid vertical
axis(2, tck = 1, lty = 2, col = "gray")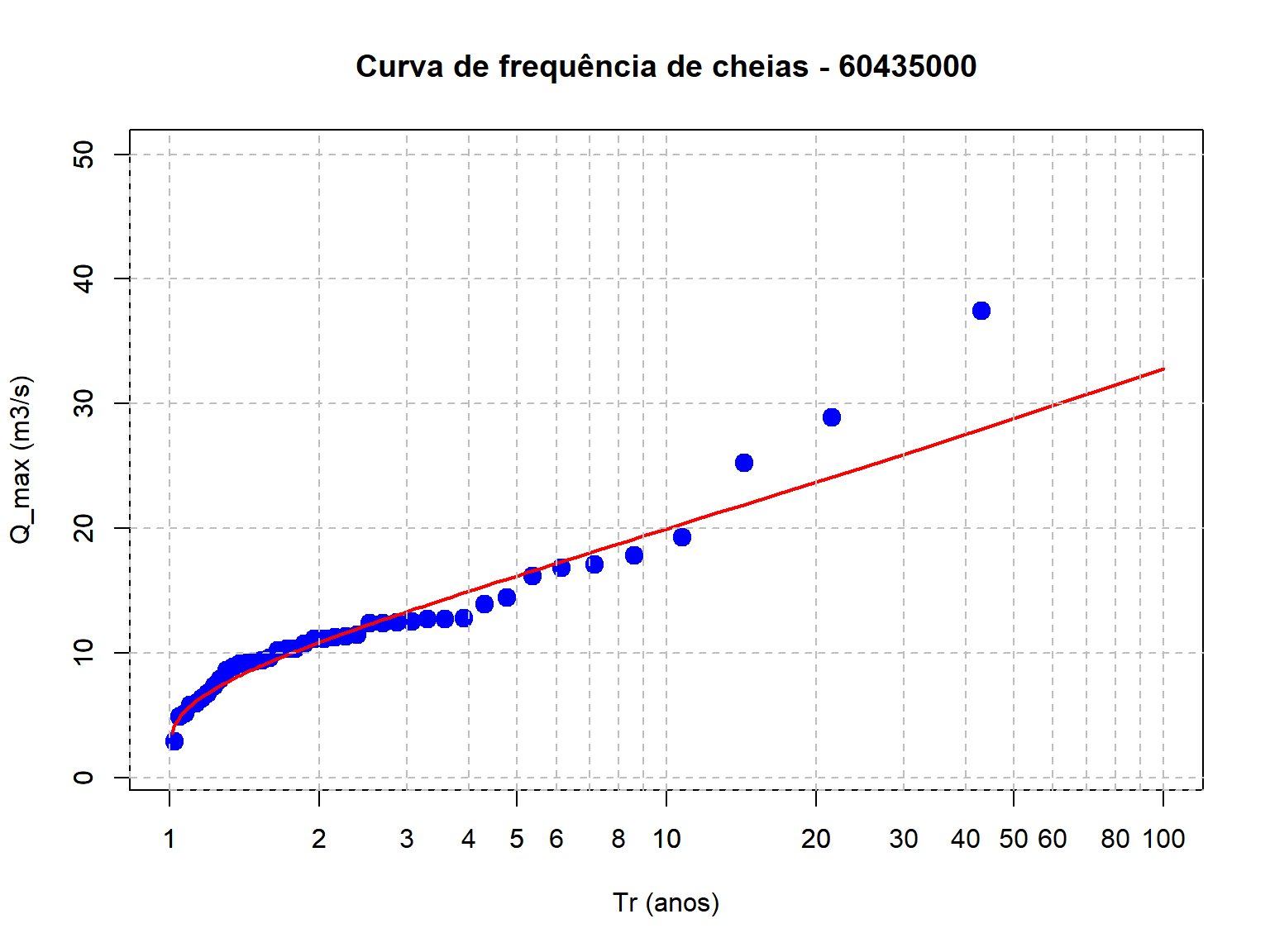
Descrição das incertezas
Quando realizamos uma análise de frequência, além da estimativa dos quantis de cheia, precisamos ter uma ideia do quão confiantes estamos em relação aos valores estimados. Sendo assim, precisamos entender como calcular a precisão dessas estimativas.
Normalmente, a maneira que empregamos para descrever as incertezas nas estimativas dos quantis de cheias é por meio de intervalos de confiança. Neste nosso exercício aqui, aprenderemos como calcular intervalos de confiança associados à distribuição lognormal, que é a distribuição que está sendo utilizada por nós para construir a curva de frequência.
Existem duas maneiras de se calcular intervalos de confiança para a distribuição lognormal,
- intervalos aproximados
- intervalos exatos
Aqui aprenderemos como determinar intervalos de confiança aproximados para os quantis de cheia oriundos da distribuição lognormal.
Lógica da construção de intervalos de confiança aproximados
Suponha que tenhamos uma estimador qualquer denominado \(\hat{W}_p\). Estou usando a variável \(W\) apenas para reforçar a ideia de que não precisa ser aquele estimador apresentado anteriormente, \(\hat{Q}_p = exp(\hat{\mu}_Y + Z_p\hat{\sigma}_Y)\), embora possa ser.
Como um estimador depende da amostra que se tem em mãos, ele é também uma variável aleatória. E como toda variável aleatória, seu comportamento pode se descrito por uma distribuição teórica de probabilidades.
Para a quase totalidade de possíveis estimadores, quando \(n\rightarrow \infty\), ou em outras palavras, à medida que a amostra aumenta e passa a ter um número bem grande de observações, esses estimadores tendem a ter uma distribuição Normal.
Bem, se \(\hat{W}_p\) possui distribuição Normal e variância \(V(\hat{W}_p)\), então nós já sabemos que se subtrairmos seu valor esperado, \(E[\hat{W}_p]\), e dividirmos o resulto pelo seu desvio-padrão, \(\sqrt{V(\hat{W}_p)}\), obteremos uma variável Normal-padrão, usualmente denominada de \(Z\),
\[ Z = \frac{\hat{W}_p-E[\hat{W}_p]}{\sqrt{V(\hat{W}_p)}} \] Como \(Z\sim N(0,1)\), podemos afirmar que a probabilidade de \(Z\) estar entre os quantis \(Z_{\alpha/2}\) e \(Z_{1-\alpha/2}\) vale \(1-\alpha\),
\[ P(z_{\alpha/2}\le Z \le z_{1-\alpha/2}) = 1-\alpha \] Se substituirmos \(Z\) da equação acima pela equação anterior, obtemos
\[ P\Bigg(z_{\alpha/2}\le \frac{\hat{W}_p-E[\hat{W}_p]}{\sqrt{V(\hat{W}_p)}} \le z_{1-\alpha/2}\Bigg) = 1-\alpha \] Depois de algumas manipulações algébricas, e admitindo que o estimador \(\hat{W}_p\) é não-tendencioso, o que significa dizer que \(E[\hat{W}_p]=W_p\), chegamos à afirmação abaixo,
\[ P\Bigg(\hat{W}_p - z_{1-\alpha/2}\sqrt{V(\hat{W}_p)} \le W_p \le \hat{W}_p + z_{1-\alpha/2}\sqrt{V(\hat{W}_p)}\Bigg) = 1-\alpha \] que em bom português diz que a probabilidade do valor populacional de \(W_p\) estar entre esses dois limites, \(\hat{W}_p \pm z_{1-\alpha/2}\sqrt{V(\hat{W}_p)}\), é igual à \(1-\alpha\). Quando \(\alpha = 0.05\), essa probabilidade vale 0.95.
É essa afirmação matemática que nos permite estabelecer o intervalo de confiança de \(100(1-\alpha)\%\) para \(W_p\), apresentado abaixo,
\[ \Bigg[\hat{W}_p - z_{1-\alpha/2}\sqrt{V(\hat{W}_p)};\hat{W}_p + z_{1-\alpha/2}\sqrt{V(\hat{W}_p)}\Bigg] \]
Estimadores intervalares para \(Y_p\) e \(Q_p\)
A expressão acima pode ser utilizada para construir o intervalo de confiança aproximado de \(Y_p=ln(Q_p)\) e de \(Q_p\), sendo esse último o que de fato nos interessa.
Primeiro, constuímos o intervalo de confiança aproximado de \(Y_p\),
\[ \Bigg[\hat{Y}_p - z_{1-\alpha/2}\sqrt{V(\hat{Y}_p)};\hat{Y}_p + z_{1-\alpha/2}\sqrt{V(\hat{Y}_p)}\Bigg] \]
Mas veja que embora tenhamos definido quem é \(V(\hat{Y}_p)\), ainda não comentamos como podemos calcular essa grandeza, e sem ela não temos como determinar, de fato, o intervalo de confiança.
Este não é um curso de estatística, mas sim de R aplicado à Hidrologia. De todo modo, deixarei aqui uma breve explicação de como obter \(V(\hat{Y}_p)\) para aqueles interessados nos detalhes da metodologia,
\[ \begin{align} V(\hat{Y}_p) &= V(\hat{\mu}_y + z_p\hat{\sigma}_Y)\\ &= V(\hat{\mu}_y) + V(z_p\hat{\sigma}_Y)\\ &= V(\hat{\mu}_y) + z_p^2V(\hat{\sigma}_Y)\\ &= \frac{\hat{\sigma}_Y^2}{n} + z_p^2V(\hat{\sigma}_Y) \end{align} \]
Para finalmente encontrar uma expressão para \(V(\hat{Y}_p)\), precisamos ainda entender como determinar \(V(\hat{\sigma}_Y)\). Para isso, recorremos ao trabalho de Ahn & Fessler (2003), que nos mostraram que \(V(\sigma_Y)\approx \hat{\sigma}_Y^2/(2n)\), o que resulta na seguinte expressão para \(V(\hat{Y}_p)\),
\[ V(\hat{Y}_p) \approx \frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_p^2\Bigg) \]
Dessa forma, o intervalo de confiança de \(100(1-\alpha)\%\) aproximado para \(Y_p\) pode ser descrito como
\[ \Bigg[\hat{Y}_p - z_{1-\alpha/2}\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_p^2\Bigg)};\hat{Y}_p + z_{1-\alpha/2}\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_p^2\Bigg)}\Bigg] \]
Para determinar o intervalo de confiança de \(100(1-\alpha)\%\) aproximado para \(Q_p\), basta exponenciar o intervalo acima,
\[ \begin{align} IC_{(1-\alpha)}(Q_p) &= exp\Bigg[\hat{Y}_p \pm z_{1-\alpha/2}\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_p^2\Bigg)}\Bigg]\\ &= exp\Bigg[(\hat{\mu}_Y+z_p\hat{\sigma}_y) \pm z_{1-\alpha/2}\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_p^2\Bigg)}\Bigg] \end{align} \]
Por exemplo, suponha que queiramos estabelecer o intervalo de confiança de 95% para o quantil \(Q_{99}\), equivalente à cheia de 100 anos de recorrência. Nesse caso, \(\alpha = 0.05\) e \(p=0.99\), o que leva ao seguinte intervalo de confiança,
\[ \begin{align} IC_{.95}(Q_{0.99}) &= exp\Bigg[(\hat{\mu}_Y+z_{.99}\hat{\sigma}_y) \pm z_{.975}\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}Z_{.99}^2\Bigg)}\Bigg]\\ &=exp\Bigg[(\hat{\mu}_Y+2.326\hat{\sigma}_y) \pm 1.96\sqrt{\frac{\hat{\sigma}_Y^2}{n}\Bigg(1+\frac{1}{2}2.326^2\Bigg)}\Bigg] \end{align} \] As linhas de código abaixo permitem calcular os limites inferior e superior do intervalo de confiança aproximado para os quantis da distribuição lognornal,
Plotagem final da curva de frequência
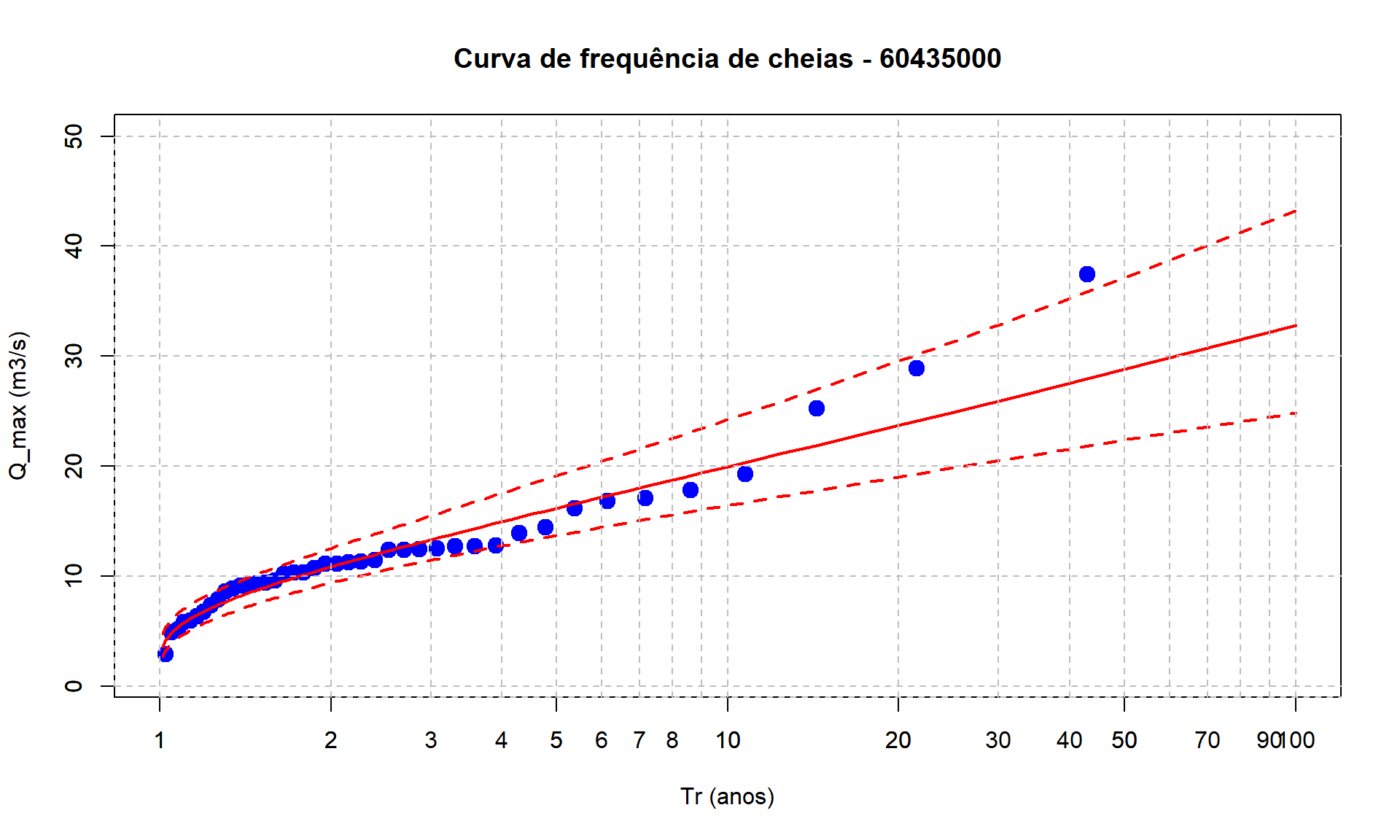
Podemos agora terminar a Figura com a nossa curva de frequência de cheias completa, incluindo os intervalor de confiança de \(95\%\) representados com a linha tracejada.
plot(Q_max_ord$Tr,Q_max_ord$maxima,type = "p", # plota apenas pontos
pch = 19,col = "blue", cex = 1.5, # círculos azuis de tamanho 1.5
log = "x", # escala logaritmica no eixo-x
main = "Curva de frequência de cheias - 60435000", # título
xlab = "Tr (anos)",ylab = "Q_max (m3/s)", # nome dos eixos
xlim = c(1, 100), # limites od eixo-x
ylim = c(1, 50)) # limites do eixo-y
# Adiciona a LN2
lines(Quantis_Q$Tr,Quantis_Q$q_p_hat,
col = "red",
lwd = 2)
# Adiciona IC
lines(Quantis_Q$Tr,lower_IC,
col = "red",lty = 2,
lwd = 2)
lines(Quantis_Q$Tr,upper_IC,
col = "red",lty = 2,
lwd = 2)
# Adiciona grid horizontal
axis(1, at = c(seq(1,10,by=1),seq(10,100,by=10),seq(200,1000,by=100)),
tck = 1, lty = 2, col = "gray")
# Adiciona grid vertical
axis(2, tck = 1, lty = 2, col = "gray")