Linguagem R

Conceitos básicos para o curso

Visão geral do R e RStudio

O que é a linguagem R

Existe um grande número de publicações sobre a linguagem R, e muitas delas podem ser obtidas de forma gratuita na internet, tudo dentro da lei, sem cometer qualquer violação de direitos autorais.

O livro abaixo é uma dessas publicações, e por se tratar de um livro digital, seu autor continua fazendo atualizações em seu conteúdo. Trata-se de uma excelente fonte de consulta, e ainda nos ensina um pouco sobre a história por detrás do desenvolvimento do R, e sua relação com a linguagem S.

Porque usar o R em Hidrologia?

Se você decidiu fazer este curso, você já deve ter uma ideia da importância de dominar uma linguagem de programação que te permita realizar suas próprias análises, aumentar sua produtividade, testar novas metodologias, ou até escrever seus próprios pacotes para serem distribuídos na internet de forma a facilitar a vida dos outros.

Mas por que o R especificamente? Para ser sincero, o mais importante, ao meu ver, é ter o domínio de uma linguagem de programação. Mas me parece bastante razoável utilizar uma linguagem que se tornou bastante popular nos útimos anos, extrapolando os limites da estatística, área genitora da linguagem.

Mas para não fugir da pergunta, seguem abaixo alguns motivos para usar a linguagem R na área de engenharia, e mais especificamente, na área de Hidrologia,

Instalação do programa

Os computadores da sala de aula do curso já têm instalado o R, assim como o RStudio. Entretanto, para que você possa se desenvolver rapidamente na linguagem, é muito importante que você tenha acesso a esses programs fora do horário do curso, ou após a Semana Universitária.

Dessa forma, sugerimos que você instale os dois programas no seu computador pessoal seguindo as instruções fornecidas nos links abaixo.

Download de 2 programas: R e RStudio

O RStudio é uma plataforma com inúmeras ferramentas úteis e que roda a linguagem R. É possível usar só o R por sua interface, mas só é possível usar o RStudio com o R instalado na máquina. Por isso, recomenda-se baixar primeiro o R e depois o RStudio.

Interface do R e RStudio

Abaixo temos a interface do R quando o baixamos. Ele é de fato o programa que rodamos e programamos com ele.

Baixamos também o RStudio, ele é uma IDE (Integrated Development Environment). Isso nada mais é do que um facilitador para usar o R, trazendo uma interface mais amigável para utilização dessa linguagem e algumas facilidades.

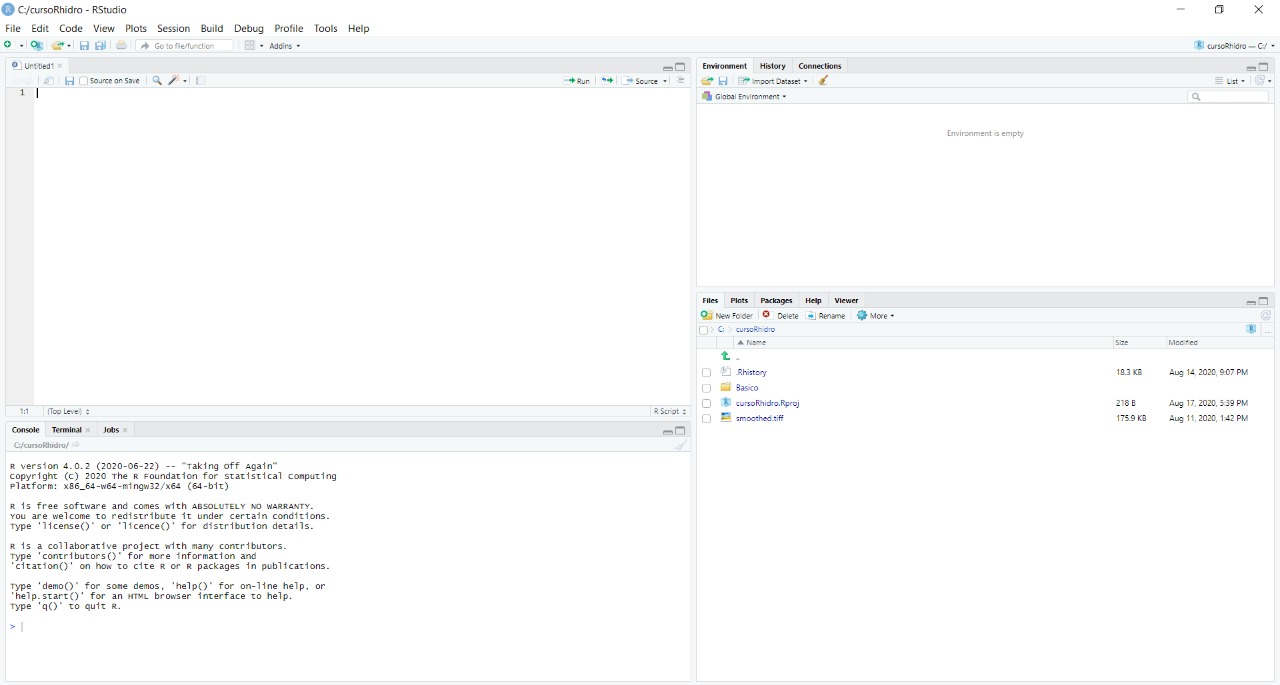
O layout é ajustável em view -> Panes -> Pane Layout

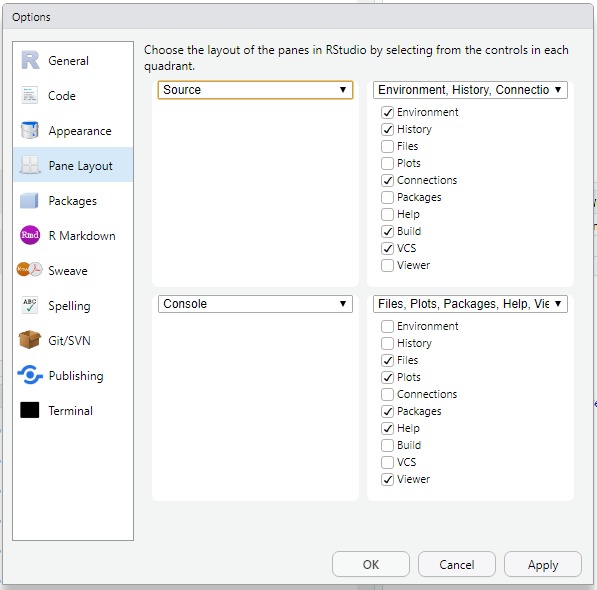
Primeiros passos e comandos no R

Antes de tudo, vale dizer que organizar seu material de trabalho enqunto utiliza o R é muito importante. E para isso, é importante que você saiba onde está trabalhando na árvore de diretórios do seu computador.

Os dois comandos abaixo ajudam nesse processo:

#getwd()
#setwd("C:/cursoR")
#dir()
#source("soma.R")

O R pode ser utilizável como uma calculadora, com os operadores aritméticos que se conhece, embora os benefícios da linguagem vão muito além dos de uma simples calculadora.

Mas vamos começar pelas operações básicas da matemática. Para multiplicação utilizamos o símbolo *, para divisão /, para expoentes ^ e para raiz quadrada usamos sqrt() - do inglês square root.

1 + 2
[1] 3
12 * 5
[1] 60
2 / 2
[1] 1
12 ^ 4
[1] 20736
sqrt(9)
[1] 3

O R trabalha igualmente com vetores e escalares. Abaixo, criamos e somamos dois vetores por exemplo.

c(1, 3, 5, 7, 9) + c(2, 4, 6, 8, 10)
[1]  3  7 11 15 19

A função c() é usada para concatenar valores, criando vetores de valores da mesma classe. Falaremos mais especificamente de classe mais à frente.

Ao usar o operador multiplicativo *, o R entende que será feita a operação elemento a elemento dentro do vetor.

c(1, 3, 5, 7) * t(c(2, 4, 6, 8))
     [,1] [,2] [,3] [,4]
[1,]    2   12   30   56

Se o objetivo, por outro lado, for o de realizar uma multiplicação de matrizes, o operador correto a ser usado é %*%, o que é muito importante na vetorização!

c(1, 3, 5, 7) %*% t(c(2, 4, 6, 8))
     [,1] [,2] [,3] [,4]
[1,]    2    4    6    8
[2,]    6   12   18   24
[3,]   10   20   30   40
[4,]   14   28   42   56

Criação de variáveis e atribuição de valores

A forma de se atribuir um valor a um elemento/objeto é utilizando o operador <-, de forma que deve haver algo dos dois lados dessa seta. De uma lado o objeto que irá receber o valor, e do outro lado o valor propriamente dito.

x <- 2
x
[1] 2

Também é possível usar o operador = para fazer isso, porém não é recomendado. Se atribuirmos algum outro valor à variável x, o valor antigo será perdido.

Veja que o R aceita trocar trocar a direção da seta, mas ela sempre deve apontar para o nome do objeto que vai receber o valor, como no exemplo abaixo,

-8 -> x
x
[1] -8

Pode-se atribuir, por exemplo, um valor não-numérico a x.

x <- "teste"
x
[1] "teste"

Alguns dos operadores que existem no R são: <-, = e ==. Como já comentado, os operadores <- e = podem ser usados para atribuir valores a variáveis/objetos, mas recomendamos utilizar sempre o <- porque o = também serve para outras coisas (falaremos disso mais a frente quando formos criar funções!).

Já o símbolo == funciona para avaliar uma igualdade e não para atribuir um valor a um elemento do R. Quando utilizamos ==, o R retorna uma variável lógica, podendo ser TRUE (verdadeiro) ou FALSE (falso). Por exemplo:

x = 2
x == 2
[1] TRUE

A segunda linha de código acima pode ser interpretada como uma pergunta que fazemos ao R, x é igual a 2? E ele responde em termos de TRUE ou FALSE.

Como neste momento, x=2, se perguntarmos se x é igual a 3, qual deve ser a resposta?

x == 3
[1] FALSE

Mas existem outros operadores lógicos que também são muito úteis, como na linha de código abaixo em que queremos saber se x é diferente de 2,

x != 2
[1] FALSE

Os operadores matemáticos >, <, >= e <= também podem ser utilizados,

x < 3
[1] TRUE
x >= 2
[1] TRUE

Objetos do R

Existem diversas classes de objetos dentro do R, alguns dos principais tipos são:

Para sabermos a classe de um objeto, podemos utilizar uma função interna do R chamada class(). Usualmente, as funções vão sempre terminar com um parêntesis (), sendo que dentro dele incluímos os argumentos da função - o que ela precisa (nesse caso, o nome do objeto). Mais à frente no curso, falaremos com maiores detalhes sobre esses argumentos, funções em geral e até mesmo como criar sua própria função.

x <- 2
class(x)
[1] "numeric"
y <- "oi"
class(y)
[1] "character"
z <- TRUE
class(z)
[1] "logical"

A forma mais básica de armazenar objetos dessas classes é na forma de vetor e os vetores podem ser criados, com a função c() já utilizada antes. A regra geral é que os vetores só armazenam objetos de mesma classe. Para criarmos um objeto contendo vários tipos de classes diferentes, podemos utilizar objetos do tipo list e dataframe, como veremos mais à frente.

Via de regra, o R enverga números quando se utiliza um valor numérico. Para se criar uma variável do tipo inteiro (integer), deve-se acrescentar a letra L ao final:

x <- 2L
class(x)
[1] "integer"

Classes de vetores

Vetores só podem conter variáveis de um tipo. Abaixo colocamos três exemplos para três tipos de classes diferentes (numérico, lógico e caractere).

x <- c(1, 2, 3, 4)
class(x)
[1] "numeric"
y <- c(FALSE, TRUE, T, F)
y
[1] FALSE  TRUE  TRUE FALSE
print(y)
[1] FALSE  TRUE  TRUE FALSE
class(y)
[1] "logical"
x <- c("ola", "bom", "dia", "programadores")
x
[1] "ola"           "bom"           "dia"           "programadores"
class(x)
[1] "character"

Fatores

O factor é uma importante classe de elemento no R para definir variáveis categóricas. São úteis em modelos de regressão linear com variáveis categóricas de entrada (estações do ano, classes de solo, cotas de alerta hidrológico etc.):

x <- factor(c("normal", "atenção", "alerta", "inundação",
              "inundação severa", "inundação", "atenção",
              "normal", "inundação", "normal", "alerta"))
x
 [1] normal           atenção          alerta          
 [4] inundação        inundação severa inundação       
 [7] atenção          normal           inundação       
[10] normal           alerta          
Levels: alerta atenção inundação inundação severa normal
table(x)
x
          alerta          atenção        inundação inundação severa 
               2                2                3                1 
          normal 
               3

Não apenas isso, mas podemos também ordenar essas classes de alguma forma, utilizando o argumento levels = para definir quais são os níveis e o argumento ordered = TRUE para mostrar que há ordem nos níveis pré-definidos.

y <- factor(c("normal", "atenção", "alerta", "inundação",
              "inundação severa", "inundação", "atenção",
              "normal", "inundação", "normal", "alerta"),
            levels = c("normal", "atenção", "alerta", "inundação", "inundação severa"),
            ordered = T)
y
 [1] normal           atenção          alerta          
 [4] inundação        inundação severa inundação       
 [7] atenção          normal           inundação       
[10] normal           alerta          
5 Levels: normal < atenção < alerta < ... < inundação severa

Coerção de variáveis

Quando se tem diferentes tipos de classes dentro de um vetor, é feita uma coerção automática para que tudo fique com a mesma classe. Dessa forma, ao criar um vetor contendo dados do tipo caractere e numérico, o R supõe que todas as informações eram para ser do tipo caractere:

x <- c("ola", 1, "dia", 2)
x
[1] "ola" "1"   "dia" "2"  
class(x)
[1] "character"

Podemos forçar uma coerção no R, a chamada Coerção explícita. Fazemos isso utilizando funções do tipo:

Com elas o R vai transformar o vetor (ou objeto) em questão no tipo que você definiu. Isso pode ser uma tarefa simples ou complicada pro programa. No exemplo abaixo, transformar tudo em caractere é relativamente fácil, o R apenas assume que o número é um string (um caractere). Dessa forma não conseguimos fazer operações aritméticas com ele, mas conseguimos fazer alguns tratamentos utilizados em texto.

x <- as.character(3)
x
[1] "3"
class(x)
[1] "character"
x + 1
Error in x + 1: argumento não-numérico para operador binário

Pdemos fazer a mesma coerção para que o vetor seja numérico. Assim iremos transformar tudo dentro do vetor como classe numérico. Nesse caso, a tarefa pro R é complicada.. afinal, como transformar “ola” em um número? Nesses casos, no lugar é retornado um valor NA (Not Available):

x <- as.numeric(c("ola", 1, "dia", 2))
Warning: NAs introduzidos por coerção
x
[1] NA  1 NA  2
class(x)
[1] "numeric"

Sequências

Podemos criar vetores sequenciais manualmente ao escrever o vetor que queremos com todos seus elementos.

x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
x
 [1]  1  2  3  4  5  6  7  8  9 10

Também podemos utilizar o símboblo : para facilitar. Assim a sequência é gerada somando um a um.

x <- c(1:10)
x
 [1]  1  2  3  4  5  6  7  8  9 10

Existe também funções para isso, como a função seq(). Com o primeiro valor sendo em qual número começamos a sequência e o segundo sendo até onde a sequêcia deve ir, sempre indo de 1 em 1.

x <- seq(1, 10)
x
 [1]  1  2  3  4  5  6  7  8  9 10

Essa função pode utilizar 3 valores. O terceiro é o tamanho do passo a ser dado, abaixo é feita uma sequência de 1 a 10, andando de 4 em 4. Ele não vai retornar 10 porque a sequência não passa por ele (ela seria 1, 5, 9, 13, 17…), mas vai retornar o maior número antes do segundo colocado dentro do seq().

x <- seq(1, 10, 4)
x
[1] 1 5 9

Indexing

Para selecionar um valor específico dentro de um vetor, se usa colchetes []. Assim, se quiser o primeiro elemento do vetor x eu escrevo x[1]. O mesmo vale para selecionar o primeiro, segundo e quinto elemento, escreveria x[c(1, 2, 5)].

x <- c(11:20)
x
 [1] 11 12 13 14 15 16 17 18 19 20
x[1]
[1] 11
x[c(1, 2, 5)]
[1] 11 12 15

Operações em ou com vetores

Podemos fazer operações com vetores igual faziamos com números no começo. Os mesmos operadores são utilizados aqui. Por exemplo, se quisermos dobrar os valores de um vetor, podemos simplesmente fazer 2* esse vetor. Em geral as operações aritméticas feitas em um vetor são feitas elementos a elementos. Para realizar operações matriciais a notação muda um pouco.

x <- c(1:5)
2*x
[1]  2  4  6  8 10
sqrt(2*x/4)
[1] 0.7071068 1.0000000 1.2247449 1.4142136 1.5811388

É possível inclusive fazer operações entre vetores. Porém, caso os vetores não sejam do mesmo tamanho teremos um problema ao fazer a operação elemento a elemento (vai acabar faltando algum). O R, nesse caso, vai fazer a operação até onde ele conseguir e irá retornar uma mensagem de aviso (Warning) - mas a conta será feita!

Abaixo tentamos somar os vetores x e y. Como o vetor y tem um elemento a menos que x, a soma vai ser feita normalmente para os primeiros 4 elementos de x, ao fazer o quinto, porém, o R vai voltar ao inicio do y - somando então o quinto elemento de x com o primeiro do y.

y <- c(1:4)
x + y
[1] 2 4 6 8 6

Podemos misturar essas operações com o indexing comentado anteriormente. Por exemplo, se quisermos saber quais valores do vetor x são maiores que 6 posso escrever como abaixo. É retornado apenas uma sequência de valores TRUE ou FALSE para cada elemento do vetor.

x > 6
[1] FALSE FALSE FALSE FALSE FALSE

Se quiser saber quantos valores dentro do meu vetor são maiores do que 4, ao invés de contar na mão posso usar a função sum()! Isso acontece porque os valores lógicos também funcionam como números, os valores TRUE são equivalentes a 1 e valores FALSE são iguais a 0. Assim somando os valores TRUE, conseguimos saber quantos números dentro do vetor x são maiores que 4.

sum(x > 4)
[1] 1

Abaixo, fazemos quais são os valores desse vetor que são maiores do que 4.

x[x > 4]
[1] 5

Também podemos juntar diversos operadores lógicos com os símbolos de & (E) e | (OU). Por exemplo, queremos saber quais elementos do vetor x são maiores do que 2 E menores que 4.

x > 2 & x < 4
[1] FALSE FALSE  TRUE FALSE FALSE

Outros tipos de dados (Data Frames, matrizes e listas)

Data Frames

Quando são lidos objetos externos (planilhas excel, arquivos .txt ou .csv), usando as funções do R read.table() ou read.csv(), por exemplo, o objeto criado é um data.frame.

A classe de data.frame é muito utilizada em R. É o que se utiliza para dados tabulados. Além disso, todos os elementos do data.frame têm o mesmo comprimento.

DF <- data.frame(x = c(1:3), coluna_2 = c("A", "B", "C"))
DF
  x coluna_2
1 1        A
2 2        B
3 3        C
class(DF)
[1] "data.frame"

Coerção de classe para data.frame.

m <- matrix(c(1:9), nrow = 3)
m <- as.data.frame(m)
m
  V1 V2 V3
1  1  4  7
2  2  5  8
3  3  6  9

Coerção de classe para data.frame.

m <- matrix(c(1:9), nrow = 3); attributes(m)
$dim
[1] 3 3
attributes(as.data.frame(m))
$names
[1] "V1" "V2" "V3"

$class
[1] "data.frame"

$row.names
[1] 1 2 3

Matrizes

Matrizes são objetos objetos semelhantes a vetores, entretanto, com o atributo dimensão dim.

m <- matrix(nrow = 2, ncol = 3); m
     [,1] [,2] [,3]
[1,]   NA   NA   NA
[2,]   NA   NA   NA
attributes(m)
$dim
[1] 2 3

Matrizes podem ser criadas a partir de vetores, adicionando o atribuito dimensão.

m <- matrix(x, nrow = 2, ncol = 5); m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    5    2    4
[2,]    2    4    1    3    5
m <- matrix(x, nrow = 2, ncol = 5, byrow = TRUE); m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    1    2    3    4    5

Para selecionar elementos de uma matriz, é necessário especificar as duas dimensões:

m <- matrix(1:4, nrow = 2); m
     [,1] [,2]
[1,]    1    3
[2,]    2    4
m[2,2]
[1] 4

Selecionar elementos de matrizes quadradas:

lower.tri(m)
      [,1]  [,2]
[1,] FALSE FALSE
[2,]  TRUE FALSE
upper.tri(m)
      [,1]  [,2]
[1,] FALSE  TRUE
[2,] FALSE FALSE

Selecionar elementos de matrizes quadradas:

m[lower.tri(m)] <- NA; m
     [,1] [,2]
[1,]    1    3
[2,]   NA    4
diag(m) <- NA; m
     [,1] [,2]
[1,]   NA    3
[2,]   NA   NA

Vetores podem ser unidos a fim de criar uma matriz:

x <- c(1:10)
y <- rnorm(10, 10, 5)
uniao <- cbind(x, y)
uniao
       x          y
 [1,]  1  7.7330320
 [2,]  2  9.1928844
 [3,]  3 14.2197264
 [4,]  4 -0.3135483
 [5,]  5  8.4014092
 [6,]  6 10.7283991
 [7,]  7  7.5505504
 [8,]  8 16.5609138
 [9,]  9  0.8132342
[10,] 10 13.2437348
dim(uniao)
[1] 10  2

A função cbind() adiciona colunas as matrizes.

Vetores podem ser unidos a fim de criar uma matriz:

x <- c(1:10)
y <- rnorm(10, 20, 5)
uniao <- rbind(x, y)
uniao
      [,1]     [,2]     [,3]     [,4]     [,5]     [,6]     [,7]
x  1.00000  2.00000  3.00000  4.00000  5.00000  6.00000  7.00000
y 24.98981 24.18452 12.43958 16.50373 20.60246 18.31887 20.43454
      [,8]     [,9]    [,10]
x  8.00000  9.00000 10.00000
y 14.68244 25.20016 13.98503
dim(uniao)
[1]  2 10

A função rbind() adiciona linhas as matrizes.

Listas

Listas são elementos importantes na programação em R. Uma das vantagens de se saber utilizar bem esse tipo de elemento é que nelas é possível armazenar elementos de diferentes tipos (caracter, número real, inteiro, complexo, lógico).

Elas são diferentes dos vetores que, via de regra, só armazenam objetos de mesma classe.

Para criar uma lista:

x <- list(1, "Ola", 1+5i, TRUE, 4L)
x
[[1]]
[1] 1

[[2]]
[1] "Ola"

[[3]]
[1] 1+5i

[[4]]
[1] TRUE

[[5]]
[1] 4

Para selecionar dados de listas, utiliza-se o duplo cochete [[]]:

x <- list(c(1,2,3), c("Ola", "Mundo"), 1+5i, TRUE, 4L)
x[[1]]
[1] 1 2 3
x[[2]][2]
[1] "Mundo"
x[[5]] + 6
[1] 10

Programação Básica

Funções

Uma coisa essencial em qualquer linguagem de programação é a criação e utilização de funções. O R (assim como outras linguagens) já vem com diversas funções instaladas nele mesmo - chamamos isso de R base. Por exemplo, se quisermos calcular o log de algum valor, podemos utilizar a função log() colocando dentro do parênteses o valor que queremos.

log(10)
[1] 2.302585

Para saber o que é preciso colocar dentro dos parênteses, ou seja, quais os argumentos (ou inputs) que cada função toma, podemos utilizar a função args(). Usando ela com o log (dessa vez sem parênteses) dentro, podemos ver que a função toma dois argumentos: o x (valor em que se calcula o logaritmo) e a base que já vem com um valor definido de exponencial. Para se ter mais informações sobre alguma função, podemos, além de usar args() utilizar uma interrogação anterior ao nome da função (sem parêntesis), ou usar a função help(). Essas duas últimas opções são equivalentes e nos mostram a documentação feita para essa função no R.

args(log)
?log
help(log)

O segundo argumento do log() pode ser modificado, basta deixar ele explícito ao chamar a função. Não precisamos escrever qual argumento estamos utilizando desde que se siga a ordem da função (mostrada anteriormente). Caso se queira escrever os argumentos em outra ordem, é possível, mas é necessário escrever cada um deles.

Veja melhor o exemplo abaixo. O primeiro não definimos a base, portanto é usada a pré definida (exponencial). No segundo log feito, não escrevemos qual a base e qual o número que queremos o logaritmo, portanto o R assume que estamos escrevendo na ordem da função, que toma como primeiro argumento o valor e o segundo argumento a base. No terceiro exemplo trocamos as ordens dos argumentos, mas para isso precisamos deixar explícito (escrito) quem é cada um.

log(100)
[1] 4.60517
log(100, 10)
[1] 2
log(base = 10, x = 100)
[1] 2

Agora vamos fazer nossa própria função dentro do R. Para isso, primeiro definimos um nome para ser o nome da função (como fizemos com criação de variáveis / objetos), por exemplo “fun_area_circulo”. Em seguida devemos dizer que vamos criar uma função e quais os argumentos que ela toma. Para fazer o exemplo, a área de um círculo, precisamos apenas de uma informação - o raio desse círculo. Podemos fazer quantas operações quisermos dentro da função, no final o último valor será retornado por ela (podemos deixar isso explícito escrevendo return nela). Depois chamamos ela como qualquer outra função!

fun_area_circulo <- function(raio){
  area <- pi*raio^2
  return(area)
}

fun_area_circulo(5)
[1] 78.53982

Estruturas condicionais (ifelse)

Em programação, algo extremamente importante e útil são os comandos if e else (e / se). Com esses comandos, é possível rodar um pedaço de código apenas se uma condição for cumprida. Esse comando no R funciona similar a uma função, sendo então o ifelse() (tudo junto!), e toma três argumentos - um lógico (uma condição), o que fazer se o lógico for TRUE e o que fazer se o lógico for FALSE. Abaixo fazemos um exemplo utilizando o ifelse para verificar se o X é maior ou menor do que 100.

x <- 10
ifelse(x < 100, "X é menor que 100", "X é maior ou igual a 100")
[1] "X é menor que 100"
x <- 1000
ifelse(x < 100, "X é menor que 100", "X é maior ou igual a 100")
[1] "X é maior ou igual a 100"

É possível usar também só o if como um comando. Em seguida rodamos um código para que, se o X for um número não inteiro, arredondamos ele e em seguida o transformamos em inteiro.

x <- 3.7
if(class(x) != "integer") x <- as.integer(round(x))
class(x)
[1] "integer"

Loops (for e while)

A última coisa a se falar do R “básico” é a construção de loops. Eles são utilizados quando queremos repetir a mesma coisa várias vezes.

for

O for() utiliza 2 argumentos separados por in. O primeiro fala qual objeto vai ser iterado várias vezes, e o outro a faixa de valores (quantas vezes ele vai ser iterado praticamente). No exemplo abaixo vamos por exemplo variar o i (criado dentro do próprio loop) na sequência de 1 até 5. Isso é o mais importante desse tipo de loop, precisamos saber quantas vezes (1:5) iterar essa variável (nesse caso i). O resto da função é simplesmente o que vai ser iterado. No exemplo abaixo apenas printamos o valor de i quando ele varia de 1 a 5.

for(i in 1:5){
  print(i)
}
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5

while

Diferente do for, utilizamos o while quando não sabemos a priori quando queremos terminar nosso loop. Ou seja, vamos ficar repetindo o que foi feito até certa condição ser cumprida. No exemplo abaixo, printamos na tela o valor de i, sendo que a cada “rodada” aumentamos o valor de i em uma unidade. Isso é feito até o i ser menor ou igual a 5, por exemplo.

i <- 0

while(i <= 5){
  print(i)
  i <- i + 1
}
[1] 0
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/DirceuReis/Mini_Curso_UnB_SemUniv_AnaliseHidro_R, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".